质心的运动行为可以代替质点组的运动行为,质点组的质量等于质心的质量,作用在此质心的力等于系统所受到的外力矢量总和.这个结论称为系统的质心运动定理。

这个讨论包含三层含义：

（1）若一个质点系的质点原来是不动的，那么在无外力作用的条件下，这个质心的位置不变；

（2）若一个质点系的质心原来是运动的，那么在无外力作用的条件下，这个质点系的质心将以原来的速度做匀速直线运动；

（3）若一个质点在某一外力作用下做某种运动，那么内力不改变质心的这种运动，比如原某以物体做抛体运动时，突然炸成两块，那么这两块物体的质心仍然继续做原来的抛体运动。

质心不是重心，在均匀重力场中，质心和重心是一样的，质心位置的计算：

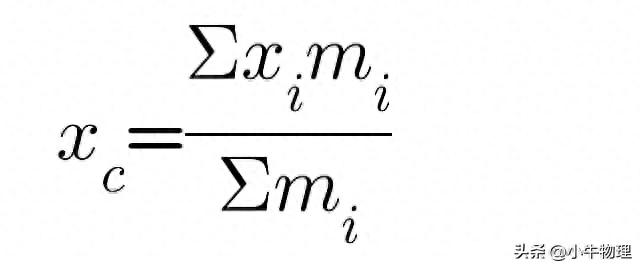
例题：有一只质量为M的小船停在静水中，船尾站一个质量为m的人，小船的长度为L。求：人从船尾走到船头，人和船所走的位移大小。（不计水的阻力）

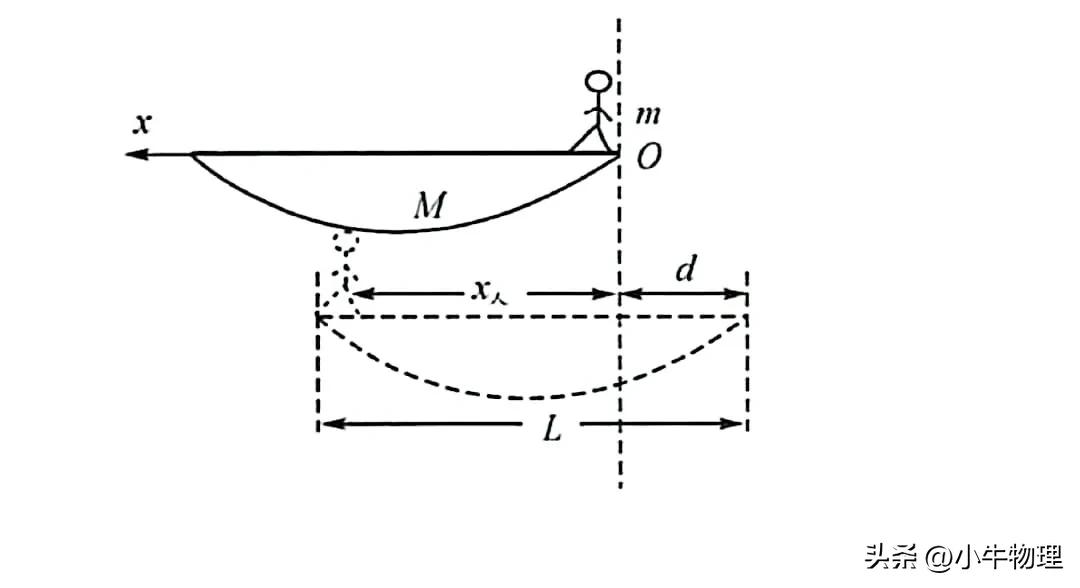
例题：如图所示，

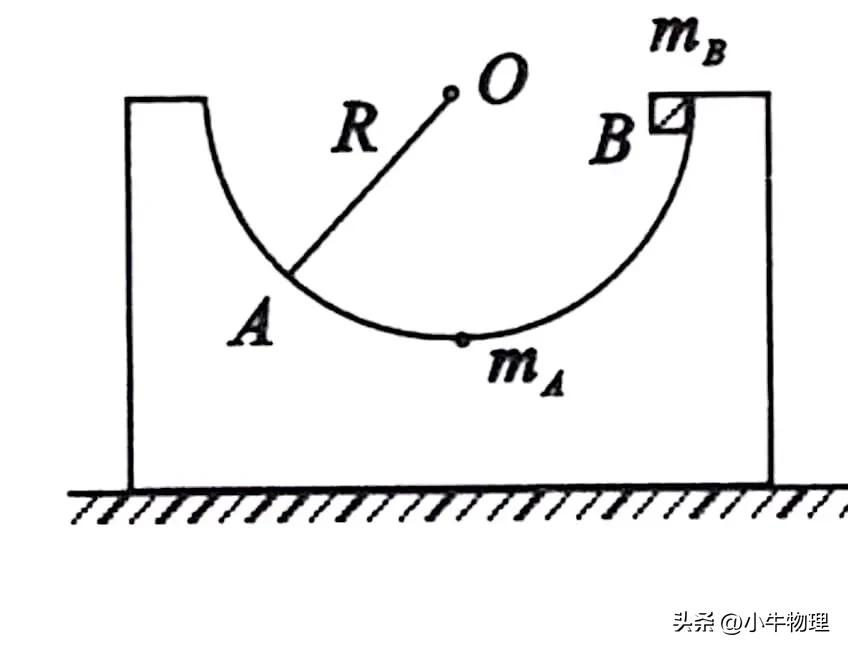
如果一个质量为mA的半圆形槽A静止在水平面上，圆槽半径为R，将一个质量为mB的小滑块B从半圆槽右上端由静止释放，若不计一切摩擦，问A的最大位移为多少？

例题：一质量为M的平板小车停在光滑的水平地面上，如图所示，

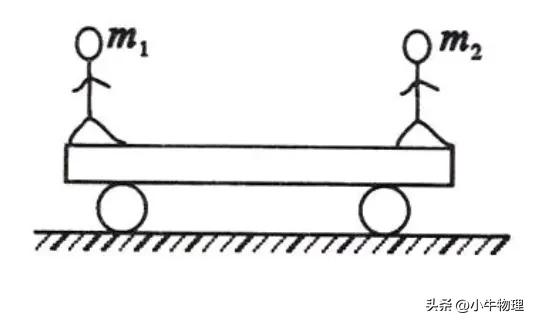
平板车长度为L.在车的左、右两端分别站立着质量为m₁和m₂的两个人（m₁＞m₂）.现两人分别向对方位置走去，当他们交换位置后，车身移动的距离为多少？

例题：如图所示，

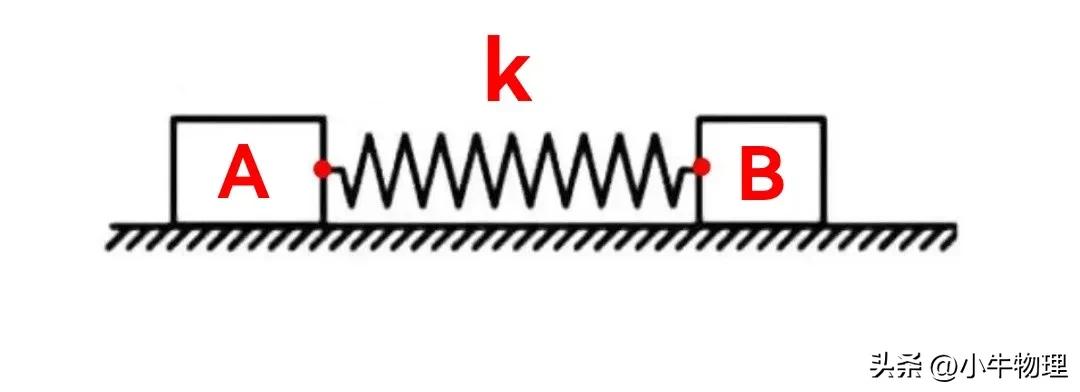
在劲度系数为k的轻弹簧两端，分别系住质量为m₁的木块A与质图量为m₂的木块B.现让两个木块将弹簧压缩后放在光滑的水平面上，求该振动系统的振动周期.

例题：如图甲所示，

小球 A 以初速度v ₀=2√gR竖直向上冲入半径为 R 的 1/4 粗糙圆弧管道，然后 从管道另一端沿水平方向以速度v₀/2= √gR冲出，在光滑水平面上与左端连有轻质弹簧的静止小球 B 发生相互作用。距离 B 右侧 s 处有一个固定的弹性挡板，B 与挡板的碰撞没有能量损失。已知 A、B 的质量分别为 3m、2m，整个过程弹簧的弹力随时间变化的图像如图乙所示（从A球 接触弹簧开始计时，t₀已知）。弹簧的弹性势能为 Ep=kx²/2，x 为形变量，重力加速度为 g。 求:

（1）小球在管道内运动的过程中阻力做的功；

（2）弹簧两次弹力最大值之比 F₂：F₁；

（3）小球 B 的初始位置到挡板的距离 s。

例题：(2015年高考安徽理综卷第12题)由3颗星体构成的系统,忽略其他星体对它们的作用,存在着一种运动形式:3颗星体在相互之间的万有引力作用下,分别位于等边三角形的3个顶点上,绕某一共同的圆心O在三角形所在的平面内做相同角速度的圆周运动(图所示为A、B、C 3颗星体质量不相同时的一般情况)．若A星体质量为2m,B、C两星体的质量均为m,三角形的边长为a,求:

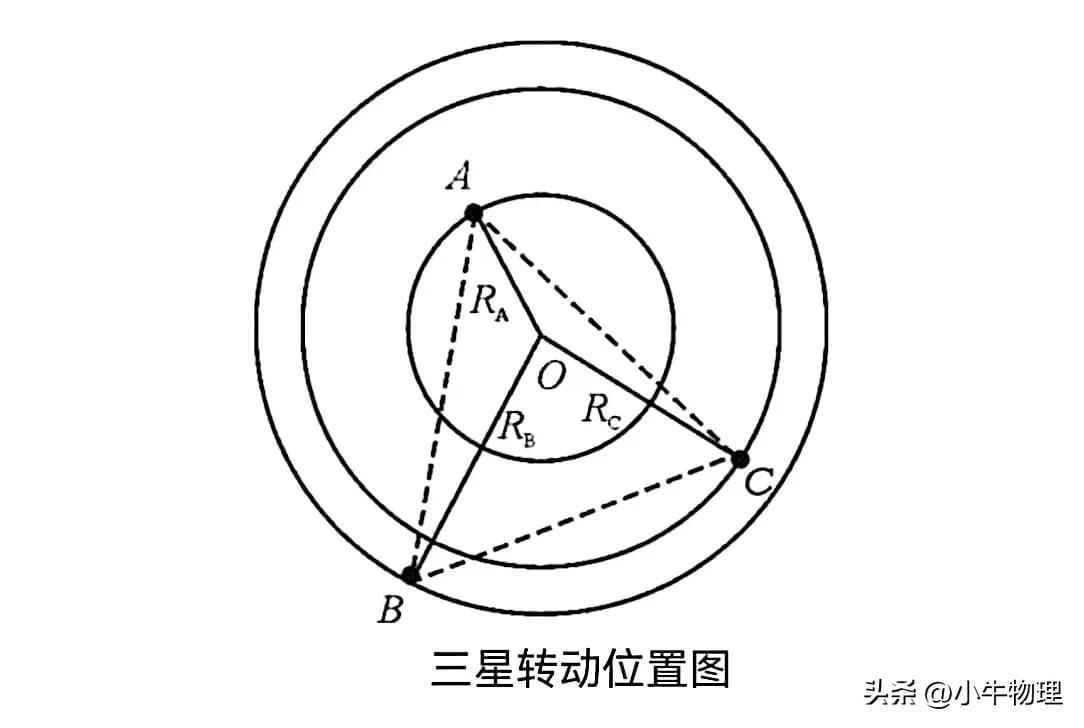
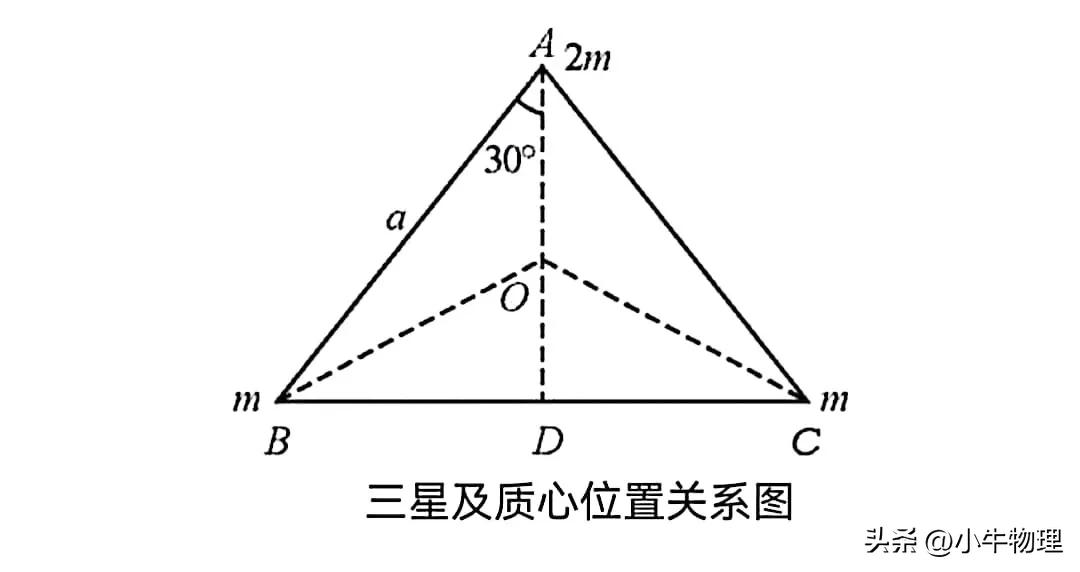
【解析】因为系统不受外力,质心加速度、速度都为零,3个星体将绕质心做匀速圆周运动,系统质心一定在BC边垂线AD的中点上,即图中的O点,A、B、C 3个星体转动的半径分别是OA、OB、OC,如图所示.

例题【练习】：如图所示,

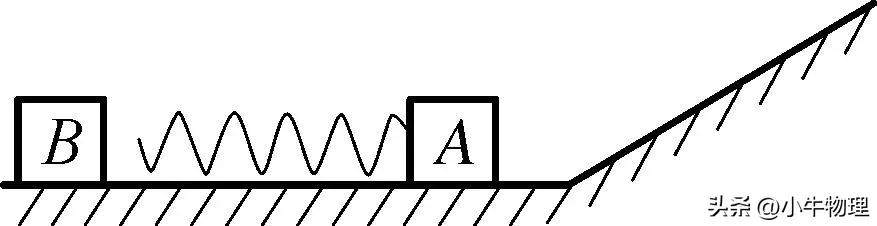
一质量为m的物块A与轻质弹簧连接,静止在光滑水平面上,物块B向A运动,t=0时与弹簧接触,到t=2t₀时与弹簧分离,第一次碰撞结束,A、B的v-t图像如图所示。

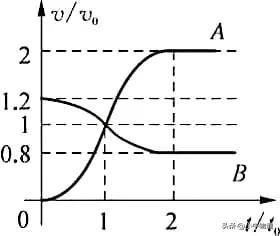
已知从t=0到t=t₀时间内,物块A运动的距离为0.36v₀t₀。A、B分离后,A滑上粗糙斜面,然后滑下,与一直在水平面上运动的B再次碰撞,之后A再次滑上斜面,达到的最高点与前一次相同。斜面倾角为θ(sinθ=0.6),与水平面光滑连接。碰撞过程中弹簧始终处于弹性限度内。求:

(1) 第一次碰撞过程中,弹簧弹性势能的最大值;

(2) 第一次碰撞过程中,弹簧压缩量的最大值;

(3) 物块A与斜面间的动摩擦因数。